Ritchie is a Data Scientist & Big Data Engineer at Xomnia. Besides working at Xomnia, he writes blogs on his website about all kinds of machine- and deep learning topics, such as: “Understanding the Fourier Transform” and “Programming a neural network from scratch”. Expect more interesting blogs from Ritchie in the future.
The Goal
Modelling a structure in Python may seem cumbersome in relation to some programs that offer a graphical user interface. For simple structures this may well be the case. However now we’ve got a simple way to programmatically model 2D structures, I was wondering if we could have a computer model these structures for us.
I’ve set the goal of building (sub) optimal bridges by letting a model determine the optimal solutions. During this process, I’ve first tried Reinforcement Learning and had limited success with that approach. A technique that had more success, and turned out to be much more simple, was Genetic Algorithms (GA). This post describes how we can have a computer find (sub) optimal solutions for our problem.
Genetic Algorithms
Before discussing the bridges let’s first have a look at the genetic algorithms model. This is actually a sort of hill climbing algorithm that tries to find the optimal solution by random changes.
Fitness
The height of the hill is described with a fitness function. If we would compare this with Darwin’s survival of the fittest, the fitness function would map your DNA to the probability of you:
- Living long enough to reproduce.
- Convincing the other sex to have coitus with you.
This guy would have a fitness score of over 9000:
And this guy would have a score of 1:
Because he misses his shot, he does get a point though.
The fitness function can be anything. It is a function that outputs positive numbers. The output of the function should be higher if the result is more optimal or closer to our desired behavior. When you want to build a bridge the fitness function could, for instance, relate to:
- Is the structure in equilibrium (does it not collapse).
- Amount of elements used (We probably don’t want to spend high material costs).
- Amount of deflection.
DNA
The input of the fitness function is DNA. For humans, DNA has 4 possible letter states. For the DNA of the bridge, we will only use one of 2 states, on or off. We can think of the DNA as a long sequence of binary values. Every index of the sequence belongs to an element on a grid. Such an element is a beam/ rod in the bridge and can be either on or off. If it is on, the element will be build. If it is off, it won’t. Simple, right?!
Let’s make it more visual with a small example. The figure below shows a grid containing possible locations to place an element. Dashed lines mean that there can be an element, but it isn’t built yet. The element locations are numbered from one to eleven.
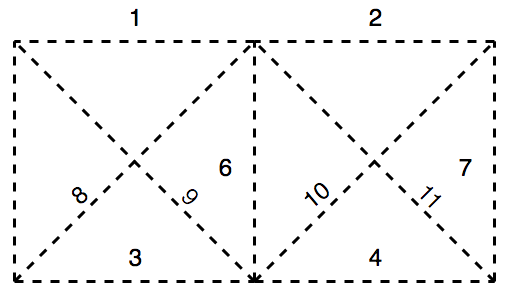
Figure 1.1 Empty grid.
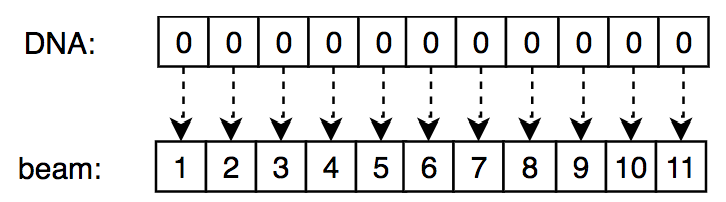
The DNA string belonging to this grid of empty elements is an array of eleven zeros. The figure below shows:
- The first row shows the DNA sequence.
- The second row shows the corresponding beam of the DNA state.
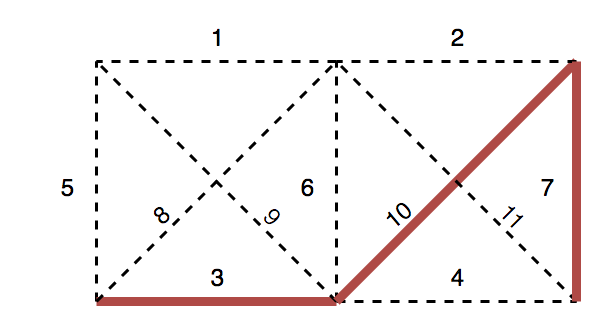
If we randomly change some DNA values from zero to one, we activate the element and the element will be deployed on the grid. The figure below shows the grid and the corresponding DNA when beam number 3, 7 and 10 are activated.
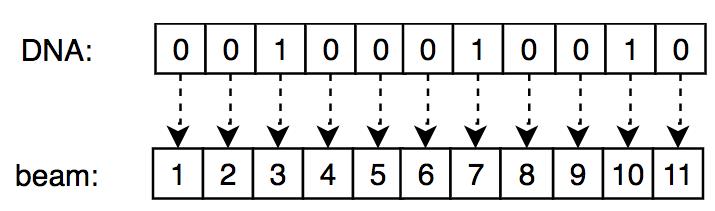
The DNA belonging to this grid is shown below.
Optimisation
This is how the DNA sequence will compare to the eventual bridge. In the first generation, the DNA will be randomly generated. The probability that a randomly generated sequence will yield a high fitness score is very low, therefore we will generate an entire population of DNA.
We can compute the fitness score for the entire population and determine which DNA sequences build better bridges than others. The first generation probably won’t contain any optimal structures. Therefore we want to be able to change the DNA randomly whilst maintaining the DNA parts that lead to a high fitness score. Genetic Algorithms are able to do so via selection, crossover, and mutation.
Selection
When the fitness of a generations population is determined, we select parents that may exchange DNA. There are different strategies for selecting parents. The chance of a parent being selected can, for instance, be proportional to their fitness score. However, when we would have a distribution with a fitness score as shown below, a selection procedure that is proportional to the fitness score would lead to a population with almost all the DNA coming from the first 2 parents.
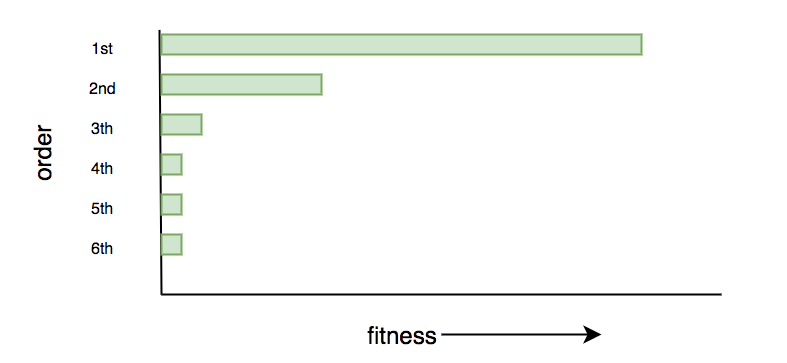
Having all the DNA coming only from a few parents, and thus having little variation in the population increases the chance of getting stuck on local maxima. In order to maintain a healthy population, the chance of being selected will be proportional the rank of the parent instead of the fitness score.
The figure below shows the selection probability being equal to the rank of the parent. We can see that the next generation will have most DNA coming from the highest scoring parent, but the low scoring parents will also contribute a significant part in the gene pool.
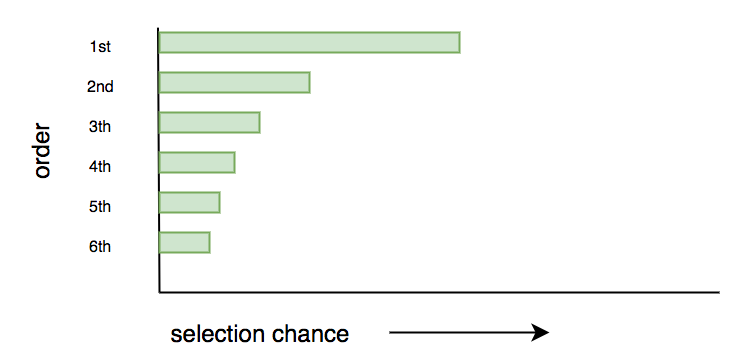
Crossover
After the selection process has succeeded (ergo you had pretty good dance moves, you didn’t stutter and you also don’t know how it has happened, but now you’re in the other person’s bed) the exchange of DNA takes place, Crossover!
Crossover can be done by combining the two DNA arrays randomly. This DNA exchange process can be done on various ways (random, the first part of the sequence, the last part of the sequence, etc.). The method I’ve used was letting a percentage of the selected parents exchange their DNA completely random.
The figure below shows how a DNA exchange could look if we randomly swap DNA parts.
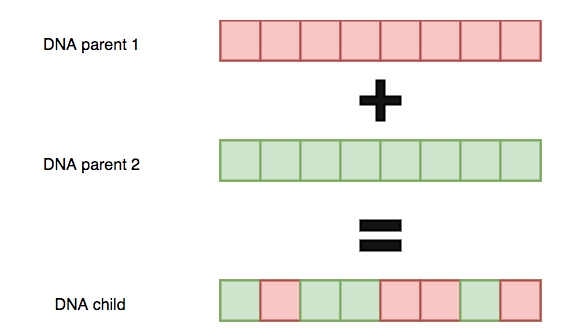
Mutation
In alignment with what I’ve learned in high school biology, during the copying of DNA there is a chance of random mutation. This random mutation makes it possible to explore new DNA states that aren’t available the gene pool of the population.
Eat, sleep, mate, repeat
These were all the steps needed for a genetic algorithm. The fitness, selection, crossover, and mutation steps will be repeated until it yields a satisfactory result, or the model is stuck on its (local) optimum.
Bridge explorations
The ideas above are reduced to code. Here you can find the script on Github. You can run different configurations by specifying:
- grid size
- stiffness
- support conditions
- unit to add in the fitness score (deflection, bending moment, axial force)
- population size
- crossover percentage
- mutation percentage
These are quite some parameters to tune. Quite logically, I’ve noticed that the fitness score is very ‘sensitive’. If it is ill-defined, you will find structures that wouldn’t seem to make any sense. But, if you regard it with the goal of maximizing that fitness score it does. In other words, the maximum fitness doesn’t always correspond with what you’ve had in mind.
The fitness score in the script is comprised of a score for:
- the amount of elements used (less is better)
- the amount of deflection or force (less is better)
- the length of the bridge (more is better)
The bridges are built symmetrically. Inspired by nature, we can save precious DNA chains by making the bridges mirror symmetrical. The DNA holds the information of the left side of the bridge, the right side is its mirror image. For every bridge, the supports are placed on the outermost nodes. The weight of the elements isn’t taken into account. The only force that applies on the bridge is a force of 100 kN, placed in the center of the structure on the most top node.
If you play with the script, you can set the bending stiffness low to simulate a truss structure. The nodes don’t completely simulate hinges. I haven’t found a proper way to implement second-order displacements in 2D FEM. If you know how, please let me know!
In the examples below animated gif images shown. You can start and pause them anytime by clicking on the image. The animation shows the best performing (i.e. highest fitness score) DNA string in the population over multiple generations. When the animation has finished, the final structure is shown.
Bridge (grid = 10×1)
Ok, let’s see what such a genetic algorithm comes up with! Shown below is the best result for a grid of 10×1, 10 units of length in the x-direction and 1 unit of length in the y-direction.
The examples below are implemented with a low bending stiffness, The bridge can thus be regarded as truss structure and is only capable of bearing axial forces.
Result on a 10×1 grid and two hinged supports.

We can see that it loses quite some elements. It also builds triangular shapes. As there is no bending capacity and the grid isn’t high enough to build a compression arch, or tension rope, this seems to be the only valid way to get a stiff structure. The tension rods that are normally in the bottom of a bending beam, don’t go all the way to the supports, contrary to what I was expecting. This is probably a better structure, regarding this fitness setting, because the supports are hinged on both sides, making it possible to build a compression arch. Let’s see the results if we change hinged support to a roller support.
Result on a 10×1 grid and a roller support.

Ok, now it has built a totally different truss bridge. Now the ratio of decreasing the deflection leads to a higher fitness score than reducing the number of elements. Let’s reduce the fitness score of the deflection by a factor 0.5.
Result on a 10×1 grid, a roller support and modified fitness score.

Alright! A genetic algorithm has the same knowledge regarding bridges as I had after structural mechanics 101. This interaction showed that you really need to hand tune the fitness function in order to get results that are in line with what you have in mind.
Some more examples
What I think is cool, is that you really see the influence of the supports in the structures that are made. With two hinged supports, you would suspect some sort of compression arch, or if you flip it a tension arch/ rope. Below you see a result of structure really exploiting the concept of compression. Note that there aren’t second-order effects like buckling, thus with this fitness score, this structure is valid.
Compression arch on a 4×3 grid

Compression arch on a 10×5 grid

If we change support condition from a hinged support fixed the x-direction, to a roller support, this compression arch concept doesn’t work anymore. Building the same kind of structure would lead to high stresses and relatively large deflections, lowering the fitness score.
In structural mechanics 201, I learned the solution to that problem. It seems the best bridge of the population also did. It builds the same kind of bridge as shown in the animation above, but because the bearings cannot support the arch thrust, it builds a tension rod (the horizontal elements on the bottom).
Tension rod on a 10×5 grid

All of the examples above were made with very low bending stiffness, simulating truss structures. If we run the same grid with a high bending stiffness, we don’t need any triangles to get a stiff structure. The algorithm finds the same conclusions, as is shown in the animation below. And here it also finds the solution to the arch truss problem by applying a tension rod.
Tension rods with bending stiff elements on a 10×5 grid

Conclusion
Genetic algorithms are a fun way of exploring parameter spaces based on a fitness score. The examples I’ve shown, were all generated while optimizing a fitness score based on the amount of deflection and the number of elements. We could optimize for other things too, as the fitness function is something we define. If we can describe our problem properly in a fitness function, a genetic algorithm can explore parameter space for us.
The drawback of this method is that every time we define a new grid, bending stiffness, support condition, or any other constraint, the algorithm requires quite some compute in order to find a (optimal) solution.
What we really want is a model that maps from these constraints to bridge configurations. Such a model only needs to train once, and can later instantly map constraints to bridge configurations. As I mentioned at the beginning of the blog, I’ve tried this with a reinforcement learning approach, but didn’t have very much success. Maybe a genetic algorithm can also be a solution to that problem?


