By performing tedious tasks, autonomous learning can save us a lot of time and effort. It can also account for its own control engineering, which is a labor-intensive task, and even attain and retain optimality in changing environments! Now isn't this something?
As useful as they might be, however, autonomous learning methods, such as Reinforcement Learning (RL) and Deep Reinforcement Learning (DRL), require huge amounts of experience before they become useful. This challenges their efficiency in being implemented to solve everyday problems. In the words of Google Brain’s co-founder Andrew Ng: “RL is a type of machine learning whose hunger for data is even greater than supervised learning. [...] There’s more work to be done to translate this to businesses and practice.”
Therefore, for DRL algorithm to achieve actual feasibility, the speed by which it learns needs to be addressed - which is also known as sample efficiency. Otherwise, DRL will be only limited to the most expensive applications in the world, such as backflipping robots.
In this blog, we will elaborate on what Reinforcement Learning, Deep Learning, and Deep Reinforcement Learning are, and explain the challenges facing them. Next, we will evaluate the effects of incorporating Reinforcement Learning from Human Feedback (RLHF) and Predictive Probabilistic Merging of Policies (PPMP) into the learning process of an algorithm, and what it does to the accuracy and speed of a Reinforcement Learning algorithm.
Join the leading data & AI consultancy in the Netherlands. Click here to view our vacancies
What are Reinforcement Learning, Deep Learning, and Deep Reinforcement Learning?
Reinforcement Learning (RL) is the process whereby an agent interacts with an environment and then obtains a reward signal that reflects upon how this agent is doing with respect to its task. RL algorithm’s objective is to maximize these rewards by selecting actions that lead to desirable outcomes, without prior knowledge.
Deep Learning (DL) is a method to approximate arbitrary functions from input-output data pairs. It involves neural networks, and is therefore suitable for high-dimensional and possibly unstructured data.
Deep Reinforcement Learning (DRL) combines reinforcement learning and deep learning, as it uses neural networks to approximate one or more mappings in the RL framework. DRL is quite a generic approach, and therefore suits a broad range of possible applications. To name a few, DRL has been applied in autonomous driving, drug dosing (e.g. cancer treatments), optimization of heat management for Google’s data centers, natural language text summarization, battling against cyber security threats, and robotic control challenges such as opening doors.
What are the limitations of (Deep) Reinforcement Learning?
Some of the challenges that Reinforcement Learning and Deep Reinforcement Learning have face are the need for excessive training, and unexpected output. Before diving into possible solutions for such problems, let’s explore those particular challenges a bit more:
1) Lots and lots of training
Because they need lots of training, Deep RL and RL applications are an expensive solution, and can sometimes be even unfeasible because the required interactions take up too much time or test setups. By advancing algorithms, we can partly overcome the need for excessive training, but not completely. his is because a fundamental issue remains: As it starts learning, a tabula-rasa agent does not have the slightest idea of how its goal is formulated, nor does it have simple notions such as gravity, nor the insight that things may break under impact. It's just a blank slate, and therefore, its first attempts will always be extremely ignorant, no matter how smart the learning is.
2) Inappropriate / useless output
Also, Deep RL and RL applications do not always provide the output you were looking for. We are probably all blown away by how smart language models like ChatGPT are, but frequently these large language models just try to reproduce the training corpus, so a challenge is to make them more specific, and thus more useful.
Don't miss Xomnia's events about the latest trends and news in the world of AI. Click here.
Incorporating human feedback to speed up DRL and RL
Even though computers have greater precision and responsiveness, humans have better insight. Therefore, the combined learning potential is greater than the sum of its parts, and we can overcome much of the sample efficiency struggles of DRL and RL by incorporating human feedback. So the goal is to improve the performance of these algorithms by leveraging human expertise.
RLHF is a process that integrates human feedback into the learning process of a reinforcement learning algorithm. It involves several components, including the RL algorithm itself, human evaluators who provide feedback, and a reward model:
- Reinforcement Learning model: We need a Reinforcement Learning model that learns based on its interaction with the environment and on human feedback.
- Human evaluators: Human evaluators play a crucial role in RLHF by providing feedback on the quality of the RL algorithm’s output. This feedback can be in the form of explicit ratings, pairwise comparisons, rankings, or other structured formats. Note: Ensuring the quality of the collected data is a significant challenge in RLHF because it requires dynamically gathering human preferences. Clear instructions and guidelines are crucial to minimize biased preferences among evaluators.
- Reward Model: The reward model is a separate model trained using the human feedback data. It fine-tunes the initial RL algorithm by adjusting the rewards assigned to different outputs. In case of an accept versus reject feedback type, the reward model is trained to predict the difference in rewards between the chosen and rejected samples. By increasing the reward distance between the chosen and rejected outputs, the reward model guides the RL algorithm to generate outputs that are more preferred by the human evaluators. Text outputs with higher rewards, as predicted by the reward model, are given higher reinforcement during training. So, it leverages human evaluators’ preferences to guide the RL algorithm’s decision-making process, ultimately leading to improved outputs. Note: Data quality is an issue, because noise, inconsistencies, or biases in the human feedback can affect the learning process. Therefore, you could consider policy optimization algorithms, for example the Proximal Policy Optimization (PPO). PPO ensures that the fine-tuning process steers the RL algorithm’s output towards higher rewards but avoids strong deviations from the original output to maintain stability and consistency.
How does Reinforcement Learning from human feedback (RLHF) differ from normal Reinforcement Learning?
The approach of aiming to enhance Reinforcement Learning by leveraging external human knowledge is called Reinforcement Learning with Human Feedback (RLHF). An example of a well-known application in which RLHF is currently used is large language models, like ChatGPT.
In normal Reinforcement Learning, an agent learns through a reward function in which rewards are derived from the environment, i.e. the current state the RL agent is in. It provides the agent with feedback in the form of rewards. The RL algorithm’s objective is to maximize these rewards by selecting actions that lead to desirable outcomes. However, the details of this learning process are not easy to reproduce, which results in a situation whereby one wants to be very accurate and precise. Moreover, because this learning process is quite opaque, it is difficult to steer it into a particular direction. RLHF, however, uses human feedback to enable steering this learning process.
We're hiring data professionals of different backgrounds! Click here.
Speeding up RL with Predictive Probabilistic Merging of Policies algorithm
Even though Reinforcement Learning with Human Feedback (RLHF) is currently hot and happening, the concept of incorporating human feedback is not new. This part of the blog provides you with a rough-around-the-edges explainer of the first algorithm to leverage directive human feedback (e.g. left/right) for DRL: Predictive Probabilistic Merging of Policies (PPMP).
Why is PPMP method worth diving into?
- You may think of it as a toolbox that enables your favorite deep actor-critic algo to process human feedback and converge much faster (it only needs to be off-policy, which is typically the case for actor-critic architectures).
- In addition, the corrections are predicted, such that the need for human feedback remains manageable.
How does Predictive Probabilistic Merging of Policies (PPMP) work?
PPMP takes a probabilistic approach whereby corrections given by the human evaluator directly affect the action selection of the agent. The philosophy behind PPMP is that while humans have superior initial performance, their final performance is typically less than that of RL, because of human’s poorer precision and greater reaction time.
Therefore, as training advances, these corrections should become more subtle. The agent’s flawed actions are probabilistically integrated with the noisy feedback, taking into account the agent's capabilities and the evaluator’s expertise. So the respective uncertainties (that reflect the abilities of the agent and the human evaluator) determine the magnitude of the corrections. That way, the initial exploration is vigorous, whereas upon convergence of the agent the corrections become more subtle such that the trainer can refine the policy.
Assuming Gaussian distributions, this principle may (for the early learning stage) be depicted as:
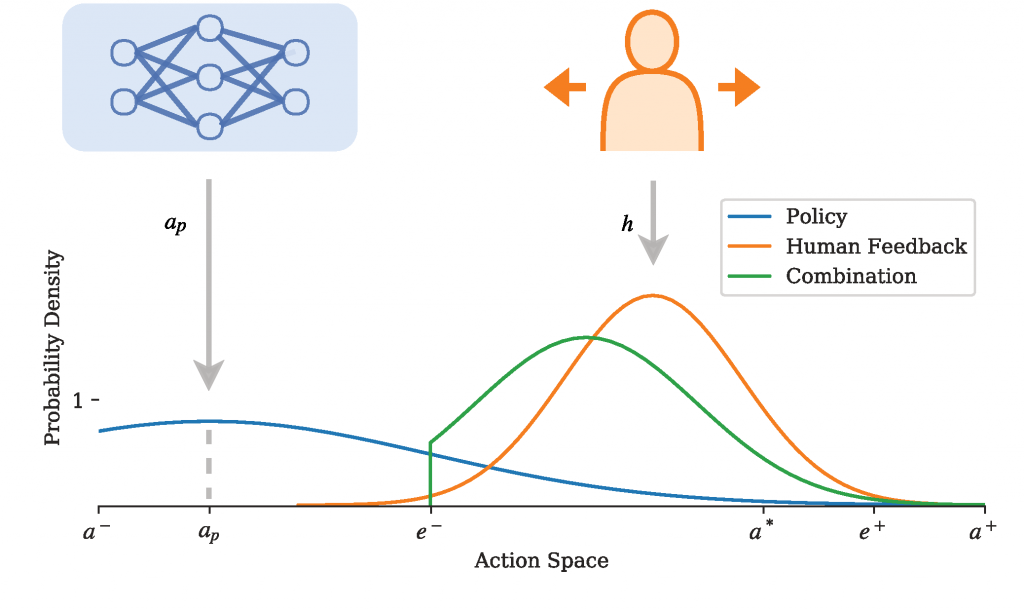
where we observe a broad distribution for rather pristine policy, and a narrower one for human feedback. The posterior estimate of the optimal action a is determined as:
where h denotes human feedback (a vector with any of -1, 0, and 1) and the estimated error
which has predefined bounds c on the correction, and then the actual tradeoff as a function of the covariances (something like a Kalman gain):
For the bounding vectors c, the lower bound expresses a region of indifference (or precision) of the human feedback. It is also assumed that the RL algorithm will effectively find the local optimum here. This is depicted by the truncated green distribution, and ensures significant effect. We may, for example, set this to a fraction of the action space. The upper bound may be used to control how aggressive the corrections can be. With the precision of the human feedback assumed as a constant (multivariate) Gaussian.
The remaining thing we need is a method to obtain up-to-date estimates of the agent's abilities. For that, we use the multihead approach from Osband et al. (2016). In actor-critic DRL, the critic and the actor are estimated using neural networks, which are a bunch of interconnected neurons. Architecture may be varied, but if we consider a simple example where the state vector x has three elements, and the action vector a two, a two-layer neural network could look like this:
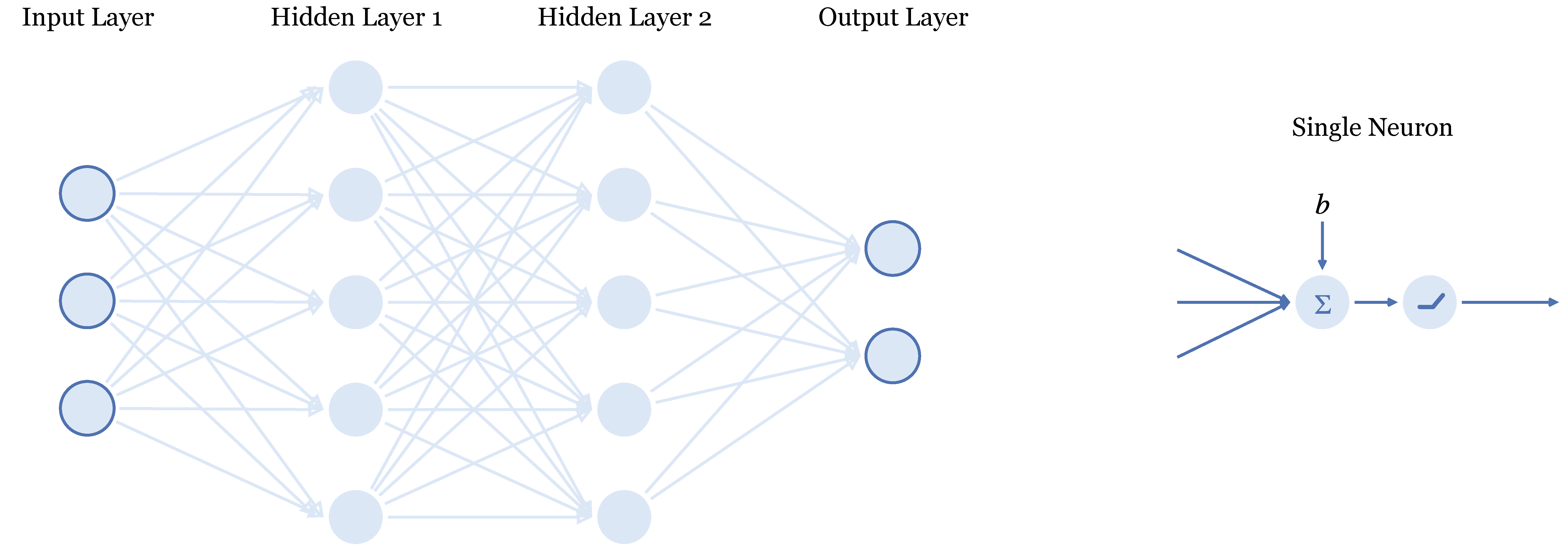
This commonplace architecture can be adapted to our need for covariance. By making a couple copies of the actors output layer (with different initial weights and training samples), we can obtain samples of the action estimate in a straightforward and efficient way. This also allows us to make inferences about the abilities of the agent by looking at the covariance between the action estimates. Observe the following scheme:
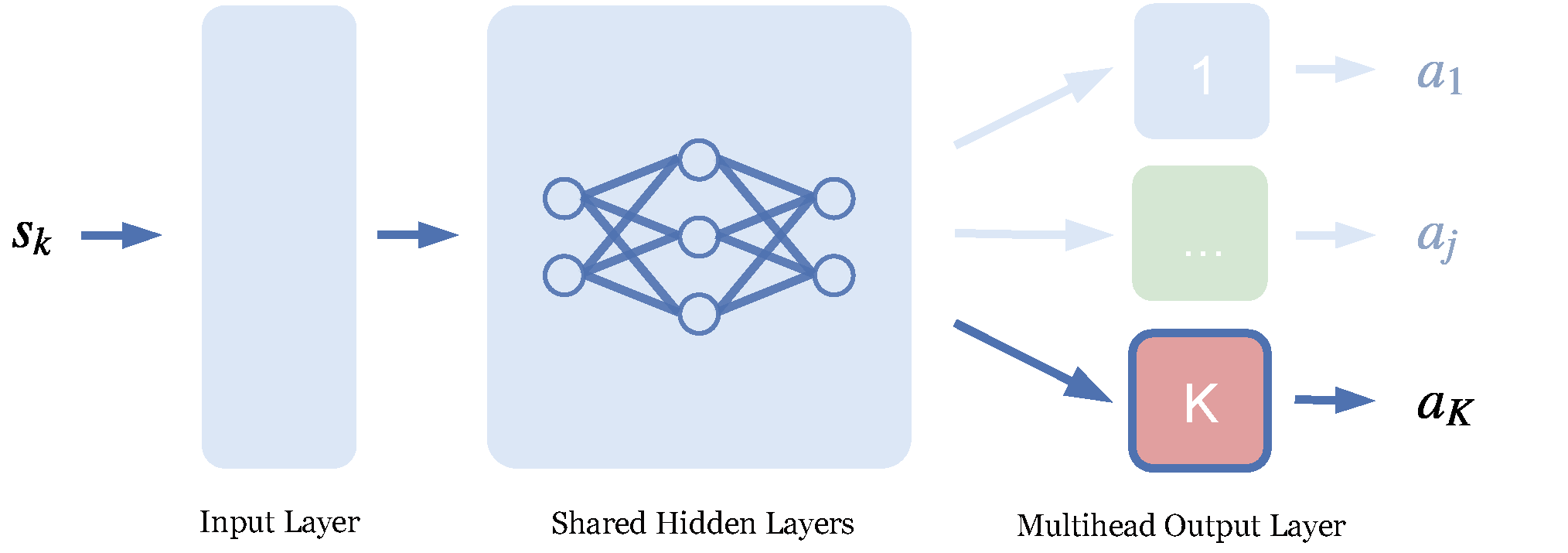
Again, under the assumption of things being Gaussian, the distribution over the optimal action estimate may now be computed as the covariance over all the heads. It leaves us with the question of what action to consider as the policy. With multimodality and temporal consistency in mind, it is best to use a designated head per episode.
Don't miss Xomnia's latest business cases and blogs. Subscribe to our newsletter.
PPMP consists of five modules, where the fifth one walks and talks:
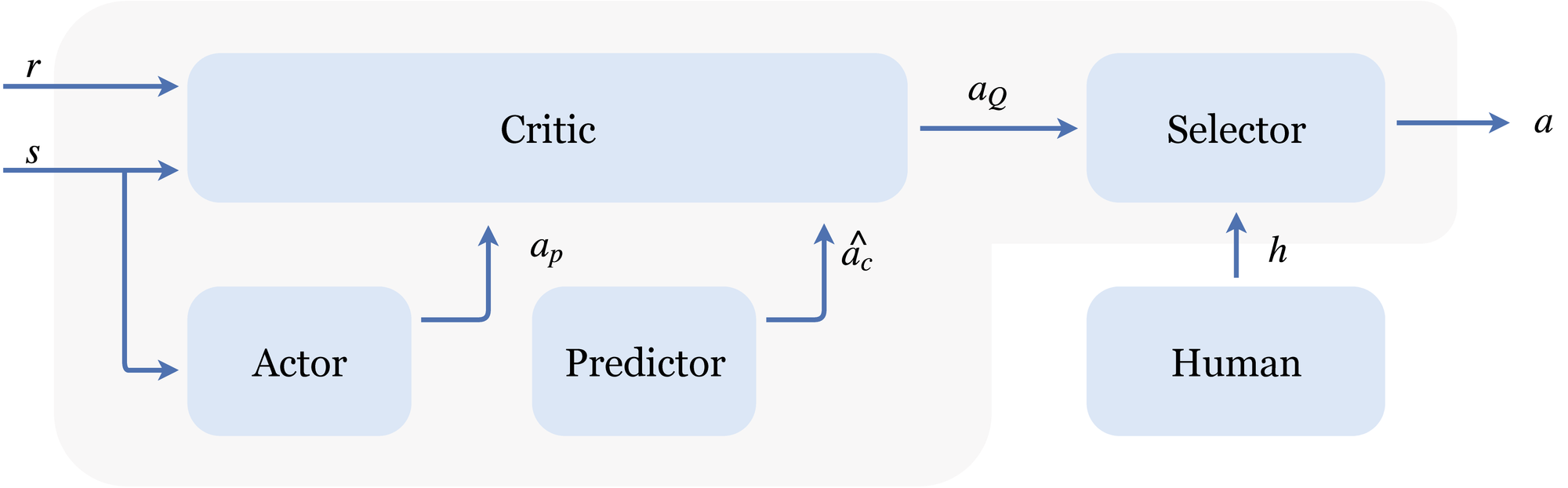
The ‘merging of policies’ as explained above happens in the ‘Selector’ module that also obtains the given feedback. To render the algorithm more feedback efficient, a ‘Predictor’ module (with the same architecture as the critic) is trained with corrected actions, such that it can provide us with rough directions --- just what we need during the earliest stages of learning.
Whilst these predicted corrected actions are very useful as a rough information source, the actions will never be very accurate. Later, when the actor’s knowledge becomes of better quality, we want to crossfade the influence from the predictor to the actor. Yet, exactly how and when the tradeoff is scheduled depends on the problem, the progress, the feedback, and most likely as well on the state. The beauty of using an actor-critic learning scheme is that we may resolve the question of how the actions should best be interleaved using the critic. It can here act as an arbiter, as it has value estimates for all state-action pairs.
Don't miss Xomnia's latest business cases and blogs. Subscribe to our newsletter.
How does PPMP perform in comparison to other Deep Learning approaches?
PPMP is benchmarked against DDPG (Deep Reinforcement Learning without human feedback, Lillicrap et al.) and DCOACH (Deep Corrective Advice Communicated by Humans, Celemin et al.), a deep learning approach that learns from corrective feedback only.
To evaluate the performance of PPMP, standard problems that require continuous control (source: OpenAI gym) were considered; as is customary in the domain of RL. The first environment, Mountaincar, requires driving a little cart up a hill and reaching the flag. Because of a little engine, the thing needs to be rocked back and forth a bit to gain momentum. The second environment is the pendulum problem, again underactuated, where a red pole is to be swung to its upright equilibrium and balanced there. Both problems penalize applied control action.
Evaluation 1: Synthesized feedback
To be able to consistently and fairly compare PPMP with other approaches without having to worry about the variance in human feedback, the model performance was evaluated using synthesized feedback with a converged DDPG policy. The following charts show the learning curves (top charts). The goal is to obtain maximum return as fast as possible for Mountaincar (left) and Pendulum (right). The charts just below show the amount of required feedback as a fraction of the samples, because the less human feedback needed the better:
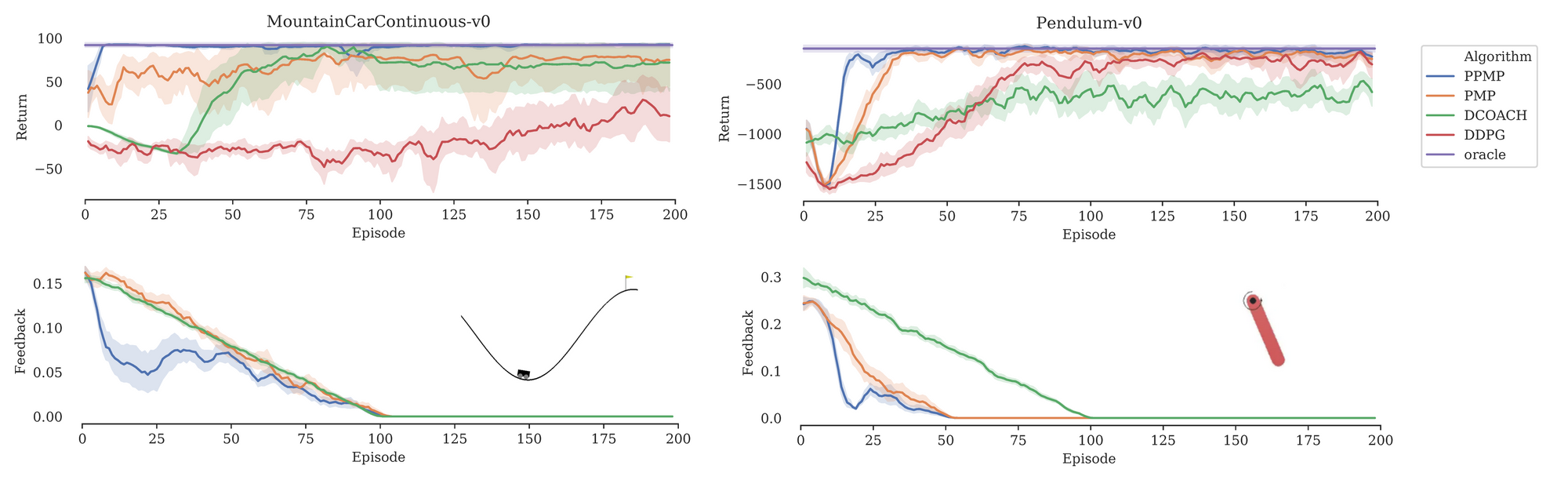
We see that DDPG (red) fails in Mountaincar. It rarely reaches the flag and therefore there is little reward. DCOACH (green) hardly solves the Pendulum problem. PPMP (blue) uses significantly less feedback but converges at least 5x faster and has superior final performance, which is on par with the oracle (purple). As an ablation study, PMP (orange) demonstrates PPMP without a predictor. For both environments, the orange curves get more feedback, but perform worse. This demonstrates that the predictor module makes the teacher’s job even easier.
Although performance is one hurdle towards making DRL work, eventual application depends as well on the robustness of algorithms. Real world problems and actual human feedback both feature real world noise, and the above innovations are only meaningful if they can cope with this noise and do not let applications crash. With the oracle implementation, we can precisely emulate erroneous feedback to assess the robustness of our algorithms. For ranges up to 30%, we stick to the previous coloring yet different line styles will now indicate the applied error rate:
It is clear that DCOACH (green) cannot handle erroneous feedback: Performance quickly drops to zero as the feedback is less perfect. Because PPMP also learns from environmental reward, it’s able to downplay the misguidance eventually and then fully solve the problem.
Evaluation 2: Noisy human feedback
Everything so far has all been evaluated based on simulated feedback. Now, what happens when we use actual human feedback that suffers from errors and delays? Below, we observe the same tendencies: Less feedback, faster learning, and greater final performance for both environments:
Last but not least, we consider a typical use case where the teacher has limited performance and is not able to fully solve the problem itself. We now consider the Lunarlander environment, a cute little game (until you actually try it), where a space pod needs to land between some flags (or it crashes). We use an oracle that more or less knows how to hover without a clue, but does not know how to safely come to a rest. The environment assigns great negative reward to crashes, and 100 points for gentle landings. PPMP compares to DDPG as follows:
Note that using DDPG, the problem is not solved. The performance difference between PPMP and its teacher may seem small when we consider the reward points, but PPMP actually found the complete solution (between the flags), thereby exceeding the performance of the teacher (purple).
Summary
We have discussed autonomous learning methods such as Reinforcement Learning (RL) and Deep Reinforcement Learning (DRL) and their potential benefits in saving time and effort by performing tedious tasks. Also, we have mentioned their challenges, including the requirement for extensive training and the potential for inappropriate or useless output. As we have seen, excessive training requirements make RL and DRL expensive and infeasible for certain applications. Inadequate output can limit the usefulness of these methods, emphasizing the need for more specific and targeted results.
A proposed solution for these issues is combining feedback from the agent’s environment with human feedback in the learning process. Human evaluators provide feedback on the quality of the RL algorithm’s output, which is used to fine-tune the algorithm’s rewards through a separate reward model. The goal is to guide the RL algorithm’s decision-making process to generate outputs that align with human preferences, resulting in improved results.
Finally, the Predictive Probabilistic Merging of Policies (PPMP) algorithm is described as a solution to incorporate human feedback in DRL. The algorithm makes corrections based on the uncertainties of the agent’s capabilities and the evaluator’s expertise. We have seen this method outperforms other deep learning approaches.
In real-world applications, assisting your model by providing it feedback can make the difference between a working robot, and a broken one, or the difference between a chatbot that generates appropriate responses, and a chatbot that generates inappropriate responses. However, ensuring the quality of human feedback data is a significant challenge. Therefore, clear instructions are necessary to minimize biases among evaluators. But also applying a method that prevents the model from strongly deviating from the original output might maintain output stability and consistency.
Join our team of top-talent data and AI professionals. Click here to view our vacancies.
Further reading
- A complete treatment of PPMP, including background on (deep) reinforcement learning, is found in the thesis titled Deep Reinforcement Learning with Feedback-based Exploration.
- PPMP was presented at the 59th Conference on Decision and Control in Nice. There’s a 6-page paper for the proceedings. (Also on Arxiv).
- The codebase of this study is hosted on github.com/janscholten/ppmp.


